已知两点 ,点
,点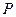 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足 .
.
(Ⅰ)求点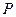 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设过点 的直线
的直线 斜率为
斜率为 ,且与曲线
,且与曲线 相交于点
相交于点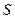 、
、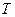 ,若
,若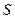 、
、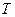 两点只在第二象限内运动,线段
两点只在第二象限内运动,线段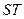 的垂直平分线交
的垂直平分线交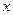 轴于
轴于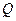 点,求
点,求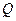 点横坐标的取值范围.
点横坐标的取值范围.
已知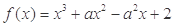 .
.
(1)若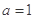 ,求曲线
,求曲线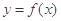 在点
在点 处的切线方程;
处的切线方程;
(2)若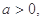 求函数
求函数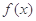 的单调区间.
的单调区间.
某公司近年来科研费用支出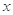 万元与公司所获得利润
万元与公司所获得利润 万元之间有如下的统计数据:
万元之间有如下的统计数据:
| x |
2 |
3 |
4 |
5 |
| Y |
18 |
27 |
32 |
35 |
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于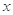 的线性回归方程
的线性回归方程 ;
;
(2)试根据(1)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:用最小二乘法求线性回归方程 的系数公式:
的系数公式: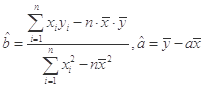
参考数据:2×18+3×27+4×32+5×35=420
设函数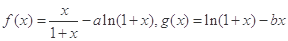 .
.
(1)若函数 在
在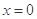 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)是否存在实数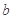 ,使得关于
,使得关于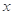 的不等式
的不等式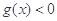 在
在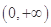 上恒成立?若存在,求出
上恒成立?若存在,求出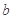 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)证明:不等式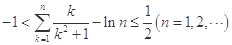 .
.
已知圆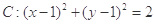 经过椭圆Γ∶
经过椭圆Γ∶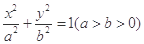 的右焦点F,且F到右准线的距离为2.
的右焦点F,且F到右准线的距离为2.
(1)求椭圆Γ的方程;
(2)过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点, 求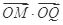 的最大值.
的最大值.
设函数f(x)=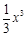 -ax,g(x)=b
-ax,g(x)=b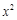 +2b-1.
+2b-1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]内的最小值.