(本题14 分)如图,五面体
分)如图,五面体
 中
中
 ,
, .底面
.底面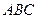 是正三角形,
是正三角形, .
. 四边形
四边形 是矩形
是矩形 ,
, 二面角
二面角
 为直二面角.
为直二面角.
(1) 在
在
 上运动,当
上运动,当 在何处时,有
在何处时,有 ∥平面
∥平面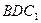 ,并且
,并且 说明理由;
说明理由;

 (2)当
(2)当 ∥平面
∥平面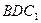 时,求二面角
时,求二面角
 的
的 余弦值.
余弦值.
三个元件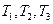 正常工作的概率分别为
正常工作的概率分别为 将它们中某两个元件并联后再和第三元件串联接入电路.
将它们中某两个元件并联后再和第三元件串联接入电路.
(Ⅰ)在如图的电路中,电路不发生故障的概率是多少?
|
(Ⅱ)三个元件连成怎样的电路,才能使电路中不发生故障的概率最大?请画出此时电路图,并说明理由.
某学生语、数、英三科考试成绩,在一次考试中排名全班第一的概率:语文为 ,
,
数学为 ,英语为
,英语为 ,问一次考试中
,问一次考试中
(Ⅰ)三科成绩均未获得第一名的概率是多少?
(Ⅱ)恰有一科成绩未获得第一名的概率是多少
奖器有 个小球,其中
个小球,其中 个小球上标有数字
个小球上标有数字 ,
, 个小球上标有数字
个小球上标有数字 ,现摇出
,现摇出 个小球,规定所得奖金(元)为这
个小球,规定所得奖金(元)为这 个小球上记号之和,求此次摇奖获得奖金数额的数学期望
个小球上记号之和,求此次摇奖获得奖金数额的数学期望
出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是相互独立的,并且概率都是
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差。
人忘记了电话号码的最后一个数字,因而他随意地拨号,假设拨过了的号码不再重复,试求下列事件的概率:
(1)第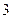 次拨号才接通电话;
次拨号才接通电话;
(2)拨号不超过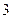 次而接通电话.
次而接通电话.