△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
(本题满分16分)已知函数
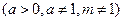 是奇函数.
是奇函数.
(1)求实数m的值;
(2)判断函数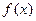 在
在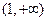 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当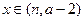 Í
Í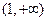 时,函数
时,函数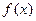 的值域是
的值域是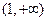 ,求实数
,求实数 与
与
(本题满分16分)已知函数
 ,在一周期内,当
,在一周期内,当 时,
时, 取得最大值3,当
取得最大值3,当 时,
时, 取得最小值-3,求
取得最小值-3,求
(1)函数的解析式.
(2)求出函数 的单调递增区间与对称轴方程,对称中心坐标;
的单调递增区间与对称轴方程,对称中心坐标;
(3)当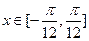 时,求函数
时,求函数 的值域
的值域
(本题满分15分)已知函数 ,
,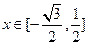
(1)当 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(2)若 在
在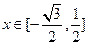 上是单调增函数
上是单调增函数 ,且
,且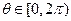 ,求
,求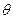 的取值范围.
的取值范围.
(本题满分15分)已知向量 ,
,
(1)若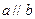 ,求实数
,求实数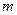 的值;
的值;
(2)若 ,求实数
,求实数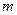 的值;
的值;
(3)若 ,且存在不等于零的实数
,且存在不等于零的实数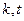 使得
使得 ,试求
,试求 的最小值.
的最小值.