(本题满分共12分)如图,在 中,
中,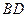 为
为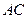 边上高,
边上高,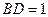 ,
,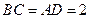 ,沿
,沿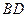 将
将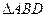 翻折,使得
翻折,使得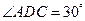 ,得到几何体
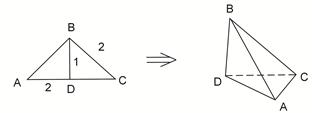
,得到几何体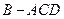 。(1)求证:
。(1)求证: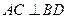 ;
;
(2)求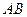 与平面
与平面 成角的正切值。
成角的正切值。
已知椭圆 ,椭圆的右焦点为F.
,椭圆的右焦点为F.
(1)求过点F且斜率为1的直线被椭圆截得的弦长.
(2)求以M(1,1)为中点的椭圆的弦所在的直线方程.
(3)过椭圆的右焦点F的直线l交椭圆于A,B,求弦 AB的中点P的轨迹方程.
已知正四棱柱 中,
中,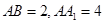 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求钝二面角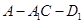 的余弦值;
的余弦值;
(Ⅲ)在线段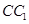 上是否存在点
上是否存在点 ,使得平面
,使得平面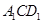
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,
的值;若不存在,
请说明理由.
已知动圆 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 的轨迹为曲线
的轨迹为曲线 ,求曲线
,求曲线 的方程.
的方程.
已知函数f(x)=x3+x-16.
(1)求满足斜率为4的曲线的切线方程;
(2)求曲线y=f(x)在点(2,-6)处的切线的方程;
(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.
请用函数求导法则求出下列函数的导数.
(1)y=esin x
(2)y=
(3)
(4)
(5)