已知椭圆 ,椭圆的右焦点为F.
,椭圆的右焦点为F.
(1)求过点F且斜率为1的直线被椭圆截得的弦长.
(2)求以M(1,1)为中点的椭圆的弦所在的直线方程.
(3)过椭圆的右焦点F的直线l交椭圆于A,B,求弦 AB的中点P的轨迹方程.
有五张卡片,它们的正、反面分别写0与1,2与3,4与5,6与7,8与9,将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
已知椭圆C1的方程为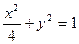 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为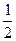 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为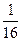 .
.
(Ⅰ)求乙投球的命中率 ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
设数列 的前
的前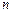 项和为
项和为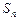 ,已知
,已知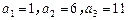 ,且
,且 ,
,
其中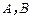 为常数.
为常数.
(Ⅰ)求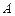 与
与 的值;
的值;
(Ⅱ)证明:数列 为等差数列;
为等差数列;
(Ⅲ)证明:不等式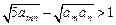 对任何正整数
对任何正整数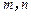 都成立.
都成立.
已知函数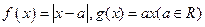 (1)判断函数
(1)判断函数 的对称性和奇偶性;(2)当
的对称性和奇偶性;(2)当 时,求使
时,求使 成立的
成立的 的集合;(3)若
的集合;(3)若 ,记
,记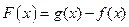 ,且
,且 在
在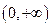 有最大值,求
有最大值,求 的取值范围.
的取值范围.