(本小题满分12分)
如图,点A,B分别是椭圆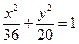 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: 且
且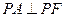 。
。
⑴求直线AP的方程;
⑵设点M是椭圆长轴AB上一点,点M到直线AP的距离等于 ,求椭
,求椭 圆上的点到
圆上的点到
点M的距离d的最小值
(本小题满分12分)已知平面向量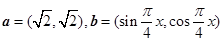
 若函数
若函数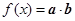 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)将函数 的图象上的所有的点向左平移1个单位长度,得到函数
的图象上的所有的点向左平移1个单位长度,得到函数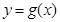 的图象,若函数
的图象,若函数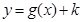 在
在 上有两个零点,求实数
上有两个零点,求实数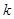 的取值范围.
的取值范围.
(本小题满分12分)在等差数列{an}和等比数列{bn}中,a1=b1=1,b4=8,{an}的前10项和S10=55.
(1)求an和bn;
(2)现分别从{an}和{bn}的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
(本小题满分7分)选修4-5:不等式选讲
已知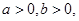 且
且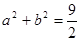 ,若
,若 恒成立,
恒成立,
(1)求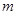 的最小值;
的最小值;
(2)若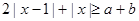 对任意的
对任意的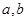 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分7分)选修4—4:坐标系与参数方程
在直角坐标系 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线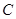 的参数方程为
的参数方程为 .
.
(1)已知在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点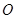 为极点,以
为极点,以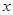 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为
的极坐标为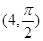 ,判断点
,判断点 与直线
与直线 的位置关系;
的位置关系;
(2)设点 是曲线
是曲线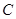 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵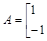
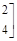 .
.
(1)求 的逆矩阵
的逆矩阵 ;
;
(2)求矩阵 的特征值
的特征值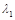 、
、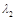 和对应的一个特征向量
和对应的一个特征向量 、
、 .
.