(本小题满分12分)
已知正项数列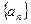 中,
中,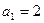 ,点
,点 在函数
在函数 的图像上,数列
的图像上,数列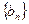 中,点
中,点 在直线
在直线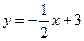 上,其中
上,其中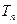 是数列
是数列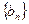 的前项和。
的前项和。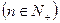 。
。
(1) 求数列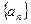 的通项公式;
的通项公式;
(2) 求数列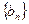 的前n项和
的前n项和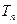 。
。
在正四面体 中,点
中,点 在
在 上,点
上,点 在
在 上,且
上,且 .
.
证明:(1)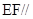 平面
平面 ;
;
(2)直线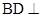 直线
直线 .
.
已知函数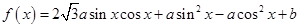 (
( ,
, ).
).
(1)若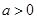 ,求函数
,求函数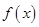 的单调增函数;
的单调增函数;
(2)若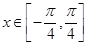 时,函数
时,函数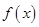 的最大值为
的最大值为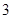 ,最小值为
,最小值为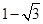 ,求
,求 ,
, 的值.
的值.
将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y-2=0与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
已知函数 (
(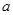 为实常数) .
为实常数) .
(1)求 的单调区间;
的单调区间;
(2)当 时,讨论方程
时,讨论方程 根的个数.
根的个数.
(3)若 ,且对任意的
,且对任意的 ,都有
,都有 ,求实数a的取值范围.
,求实数a的取值范围.
已知椭圆C的离心率为 ,直线
,直线 被以椭圆的短轴为直径的圆截得弦长为
被以椭圆的短轴为直径的圆截得弦长为 ,抛物线
,抛物线 以原点为顶点,椭圆的右焦点为焦点.
以原点为顶点,椭圆的右焦点为焦点.
(Ⅰ)求椭圆 与抛物线
与抛物线 的方程;
的方程;
(Ⅱ)已知 ,
, 是椭圆
是椭圆 上两个不同点,且
上两个不同点,且 ⊥
⊥ ,判定原点
,判定原点 到直线
到直线 的距离是否为定值,若为定值求出定值,否则,说明理由.
的距离是否为定值,若为定值求出定值,否则,说明理由.