(本小题满分12分)
如图,在直三棱柱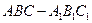 中,
中, ,
,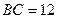
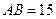 ,
,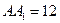 ,点D是
,点D是 的中点
的中点
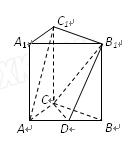
⑴求证: ;
;
⑵求证: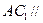 平面
平面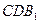 。
。
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知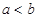 ,且
,且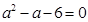 ,
, ,数列
,数列 、
、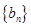 满足
满足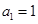 ,
, ,
, ,
,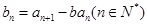 .
.
(1) 求证数列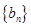 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
,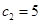 ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知函数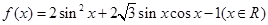 .
.
(1) 试说明函数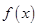 的图像是由函数
的图像是由函数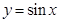 的图像经过怎样的变换得到的;
的图像经过怎样的变换得到的;
(2) (理科)若函数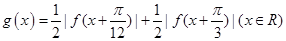 ,试判断函数
,试判断函数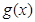 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数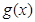 的最小正周期是
的最小正周期是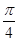 ;
;
(3) 求函数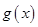 的单调区间和值域.
的单调区间和值域.
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
要测定古物的年代,常用碳的放射性同位素 的衰减来测定:在动植物的体内都含有微量的
的衰减来测定:在动植物的体内都含有微量的 ,动植物死亡后,停止了新陈代谢,
,动植物死亡后,停止了新陈代谢, 不再产生,且原有的
不再产生,且原有的 含量的衰变经过5570年(
含量的衰变经过5570年( 的半衰期),它的残余量只有原始量的一半.若
的半衰期),它的残余量只有原始量的一半.若 的原始含量为
的原始含量为 ,则经过
,则经过 年后的残余量
年后的残余量 与
与 之间满足
之间满足 .
.
(1) 求实数 的值;
的值;
(2) 测得湖南长沙马王堆汉墓女尸中 的残余量约占原始含量的76.7%,试推算马王堆古墓的年代(精确到100年).
的残余量约占原始含量的76.7%,试推算马王堆古墓的年代(精确到100年).
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
(理科)已知四棱锥 的底面
的底面 是直角梯形,
是直角梯形, ,
, ,
,
侧面 为正三角形,
为正三角形, ,
, .如图4所示.
.如图4所示.
(1) 证明: 平面
平面 ;
;
(2) 求四棱锥 的体积
的体积 .
.