阅读下面的程序框图,解答下列问题。
(1)如果输入的 的值是5,则输出的
的值是5,则输出的 值是多少?
值是多少?
(2)写出程序框图所表示的函数。
( 13分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
(12分)已知函数 ,
,
(1)判断函数 的单调性,并利用单调性定义证明;
的单调性,并利用单调性定义证明;
(2)求函数 的最大值和最小值.
的最大值和最小值.
求 值:
(1) (2)
(2)
(12分)设集合 ,全集为实数集R
,全集为实数集R
(1)求: ;
; ;
;
(2)若 ,求
,求 的取值范围
的取值范围
设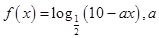 为常数,若
为常数,若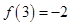 .
.
(1)求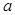 的值;
的值;
(2)求使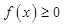 的
的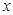 的取值范围;
的取值范围;
(3)若对于区间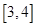 上的每一个
上的每一个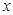 的值,不等式
的值,不等式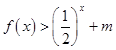 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.