如图,已知正三棱柱的底面边长为2,侧棱长为,点在侧棱上,点在侧棱上,且,.

(I) 求证:;
(II)求二面角的大小.
已知函数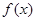 是定义在
是定义在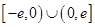 上的奇函数,当
上的奇函数,当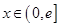 时,
时, 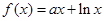 (其中e是自然界对数的底,
(其中e是自然界对数的底,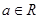 )
)
(1)设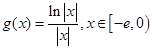 ,求证:当
,求证:当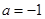 时,
时,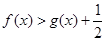 ;
;
(2)是否存在实数a,使得当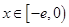 时,
时,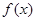 的最小值是3 ?如果存在,求出实
的最小值是3 ?如果存在,求出实
数a的值;如果不存在,请说明理
已知数列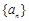 满足:
满足: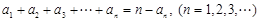
(1)求证:数列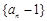 是等比数列;
是等比数列;
(2)令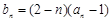 (
(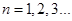 ),如果对任意
),如果对任意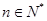 ,都有
,都有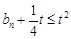 ,
,
求实数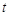 的取值范围.
的取值范围.
如图,在直三棱柱 中,
中, 分别是
分别是 的中点,且
的中点,且 .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
平面直角坐标系 中,已知向量
中,已知向量 且
且 .
.
(1)求 与
与 之间的关系式;
之间的关系式;
(2)若 ,求四边形
,求四边形 的面积.
的面积.
已知数列 满足
满足 =-1,
=-1, ,数列
,数列 满足
满足
(1)求证:数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当 时,
时,
(3)设数列 的前
的前 项和为
项和为 ,求证:当
,求证:当 时,
时, .
.