在平面直角坐标系中，直线l：交轴于点，设是上一点，是线段的垂直平分线上一点，且满足．
（1）当点在上运动时，求点的轨迹的方程；
（2）已知，设是上动点，求的最小值，并给出此时点的坐标；
（3）过点且不平行与轴的直线与轨迹有且只有两个不同的交点，求直线的斜率的取值范围．
已知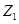
、
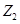是实系数一元二次方程的两个根.问是否存在这样的实数a,使得等式
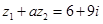总不能成立？若存在，找出所有这样的a；若不存在，说明理由.
在△ABC中，角A、B、C的对应边分别为a、b、c，若lga-lgb=lgcosB-lgcosA
(1)判断△ABC的形状；
(2)若a、b满足：函数y=ax+3的图象与函数y=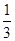
x-b的图象关于直线y=x对称，求边长c.
已知对于x的所有实数值，二次函数f(x)=x2－4ax+2a+12(a∈R)的值都是非负的，求关于x的方程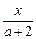
=|a－1|+2的根的取值范围.
已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，求m的范围.
(2)若方程两根均在区间(0，1)内，求m的范围.
已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R).
(1)求证:两函数的图象交于不同的两点A、B；
(2)求线段AB在x轴上的射影A1B1的长的取值范围.