设函数 定义域为
定义域为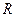 ,当
,当 时,
时, ,且对于任意的
,且对于任意的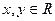 ,都有
,都有
(1)求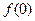 的值,并证明函数
的值,并证明函数 在
在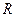 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若 时,不等式
时,不等式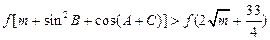 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本题满分16分)
一束光线从点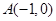 出发,经过直线
出发,经过直线 上的一点D反射后,经过点
上的一点D反射后,经过点 .
.
⑴求以A,B为焦点且经过点D的椭圆C的方程;
⑵过点 作直线
作直线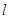 交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
(本题满分15分)
在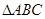 中,三边a,b,c满足:
中,三边a,b,c满足: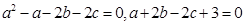 .
.
⑴探求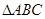 的最长边;
的最长边;
⑵求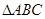 的最大角.
的最大角.
(本题满分15分)
已知三次函数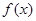 的最高次项系数为a,三个零点分别为
的最高次项系数为a,三个零点分别为 .
.
⑴ 若方程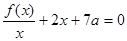 有两个相等的实根,求a的值;
有两个相等的实根,求a的值;
⑵若函数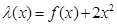 在区间
在区间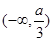 内单调递减,求a的取值范围.
内单调递减,求a的取值范围.
(本题满分14分)在三棱柱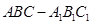 中,
中,
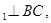
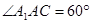 ,
,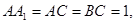
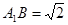
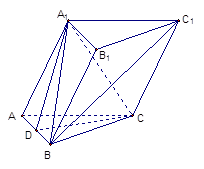
⑴求证:平面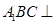 平面
平面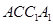 ;
;
⑵如果D为AB的中点,求证: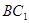 ∥平面
∥平面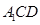
(本题满分14分)在平面直角坐标系 中,点
中,点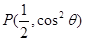 在角
在角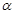 的终边上,点
的终边上,点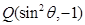 在角
在角 的终边上,且
的终边上,且
⑴求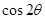 的值;⑵求
的值;⑵求 的值。
的值。