如图所示, 三个台阶每个台阶高 h="0.225" 米,宽s=0.3米。小球在平台AB上以初速度v0水平向右滑出,要使小球正好落在第2个平台CD上,不计空气阻力，求初速v0范围。某同学计算如下：(g取10m/s2)
根据平抛规律 2h=gt2/2 ；
到达D点小球的初速 vD =2s/t=2×0.3/0.3=2m/s
到达C点小球的初速 vC =s/t=0.3/0.3=1m/s
所以落到台阶CD小球的初速范围是 1m/s < v0 < 2m/s
以上求解过程是否有问题，若有，指出问题所在，并给出正确的解答。
如图10—1—1是一列向右传播的横波，请标出这列波中a、b、c、d……h等质点这一时刻的速度方向．
如图11-4-4所示，光滑的半球壳半径为R,O点在球心的正下方，一小球由距O点很近的A点由静止放开，同时在O点正上方有一小球自由落下，若运动中阻力不计，为使两球在O点相碰，小球由多高处自由落下（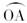
＜＜
）.
图11-4-4
试确定下列几个摆球在平衡位置附近来回振动的周期.
（1）如图11-4-3甲所示.悬挂在水平横梁上的双线摆球.摆线长为l，摆线与水平横梁夹角θ；
（2）如图11-4-3乙所示.光滑斜面上的摆球.斜面倾角为θ，摆线长为l；
（3）如图11-4-3丙所示.悬挂在升降机中的单摆，摆长为l，升降机以加速度a竖直向上做匀加速运动.
图11-4-3
将一水平木板从一沙摆（可视为简谐运动的单摆）下面以a="0.2" m/s2的加速度匀加速地水平抽出，板上留下的沙迹如图11-4-2所示，量得
="4" cm,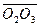
="9" cm,
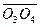="14" cm，试求沙摆的振动周期和摆长.（g="10" m/s2）
图11-4-2
有一单摆，其摆长l="1.02" m，摆球的质量m="0.10" kg，已知单摆做简谐运动，单摆振动30次用的时间t="60.8" s，试求：
（1）当地的重力加速度是多大？
（2）如果将这个摆改为秒摆，摆长应怎样改变？改变多少？