已知 、
、 分别是
分别是 的外接圆和内切圆;证明:过
的外接圆和内切圆;证明:过 上的任意一点
上的任意一点 ,都可作一个三角形
,都可作一个三角形 ,使得
,使得 、
、 分别是
分别是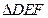 的外接圆和内切圆.
的外接圆和内切圆.
已知定义在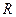 上的函数
上的函数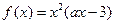 ,其中
,其中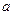 为常数.
为常数.
(1)若 是函数
是函数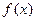 的一个极值点,求
的一个极值点,求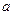 的值;
的值;
(2)若函数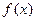 在区
在区 间
间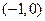 上是增函数,求
上是增函数,求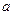 的取值范围;
的取值范围;
(3)若函数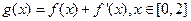 ,在
,在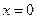 处取得最大值,求正数
处取得最大值,求正数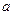 的取值范围.
的取值范围.
某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
如图,在半径为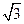 、圆心角为
、圆心角为 的扇形的弧上任取
的扇形的弧上任取 一点
一点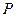 ,作扇
,作扇 形的内接矩形
形的内接矩形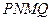 ,使点
,使点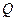 在
在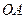 上,点
上,点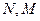 在
在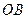 上,设矩形
上,设矩形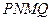 的面积为
的面积为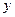 ,
,
(1)按下列要求写出函数的关系式:
①设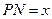 ,将
,将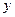 表示成
表示成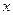 的函数关系式;
的函数关系式;
②设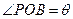 ,将
,将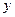 表
表 示成
示成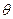 的函数关系式;
的函数关系式;
(2)请你选用(1)中的一个函数关系式,求出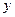 的最大值.
的最大值.
已知集合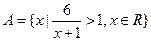 ,
,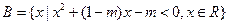 .
.
(1)若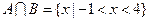 ,求实数
,求实数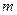 的值;
的值;
(2)当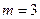 时,求
时,求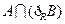 );
);
(3)若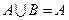 ,求实数
,求实数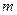 的取值范围.
的取值范围.
在平面直角坐标系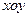 中,以
中,以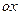 轴为始边作两个锐角
轴为始边作两个锐角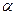 ,
,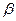 ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于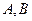 两点,已知
两点,已知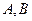 的纵坐标分别为
的纵坐标分别为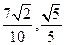 .(1)求
.(1)求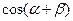 的值;(2)求
的值;(2)求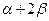 的值.
的值.