设平面上向量 与
与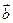 不共线,
不共线,
(1) 证明向量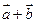 与
与 垂直(2) 当两个向量
垂直(2) 当两个向量 与
与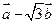 的模相等,求角
的模相等,求角 .
.
⑴用综合法证明: ;
;
⑵用反证法证明:若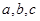 均为实数,且
均为实数,且 ,
, ,
,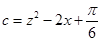 ,求证
,求证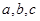 中至少有一个大于0.
中至少有一个大于0.
已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
已知向量a=(cos 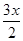 ,sin
,sin 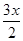 ),b=(-sin
),b=(-sin 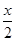 ,-cos
,-cos 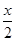 ),其中x∈[
),其中x∈[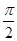 ,π].
,π].
(1)若|a+b|= ,求x的值;
,求x的值;
(2)函数f(x)=a·b+|a+b|2,若c>f(x)恒成立,求实数c的取值范围.
已知函数f(x)= cos
cos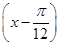 ,x∈R.
,x∈R.
(1)求f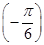 的值;
的值;
(2)若cos θ=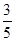 ,θ∈
,θ∈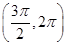 ,求f
,求f .
.