设向量 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量 ,
,
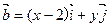 ,且
,且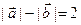 .(1)求满足上述条件的点
.(1)求满足上述条件的点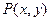 的轨迹方程;(2)设
的轨迹方程;(2)设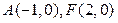 ,问是否存在常数
,问是否存在常数 ,使得
,使得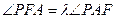 恒成立?证明你的结论.
恒成立?证明你的结论.
某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人)。求:(1)其中甲、乙两人都被安排的概率是多少?(2)甲、乙两人中至少有一人被安排的概率是多少?
甲从装有编号为1,2,3,4,5的卡片的箱子中任意取一张,乙从装有编号为2,4的卡片的箱子中任意取一张,用 ,
, 分别表示甲、乙取得的卡片上的数字.(1)求概率
分别表示甲、乙取得的卡片上的数字.(1)求概率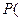

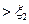 );(2)记
);(2)记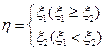 ,求
,求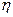 的分布列与数学期望.
的分布列与数学期望.
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.(1)求这箱产品被用户接收的概率;(2)记抽检的产品件数为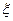 ,求
,求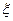 的分布列和数学期望.
的分布列和数学期望.
如图,正方形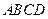 的边长为1,
的边长为1,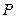 ,
,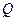 分别为边
分别为边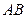 ,
,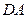 上的点.当
上的点.当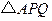 的周长为2时,求
的周长为2时,求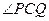 的大小.
的大小.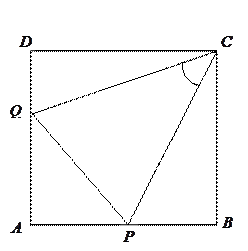

已知直线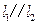 ,
,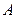 是
是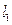 ,
,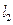 之间的一定点,并且
之间的一定点,并且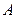 点到
点到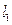 ,
,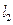 的距离分别为
的距离分别为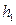 ,
,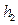 .
.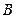 是直线
是直线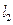 上一动点,作
上一动点,作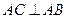 .且使
.且使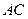 与直线
与直线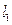 交于点
交于点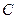 ,求
,求 面积的最小值.
面积的最小值.