甲从装有编号为1,2,3,4,5的卡片的箱子中任意取一张,乙从装有编号为2,4的卡片的箱子中任意取一张,用 ,
, 分别表示甲、乙取得的卡片上的数字.(1)求概率
分别表示甲、乙取得的卡片上的数字.(1)求概率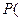

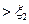 );(2)记
);(2)记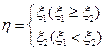 ,求
,求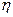 的分布列与数学期望.
的分布列与数学期望.
设 、
、 分别是椭圆
分别是椭圆  的左、右焦点,
的左、右焦点, .
.
(Ⅰ)若 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求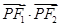 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若C为椭圆上异于B一点,且 ,求
,求 的值;
的值;
(Ⅲ)设P是该椭圆上的一个动点,求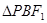 的周长的最大值.
的周长的最大值.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.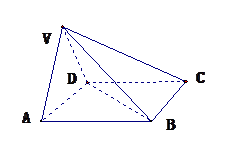
(Ⅰ)证明AB⊥平面VAD.
(Ⅱ)求面VAD与面VDB所成的二面角的余弦值.
设数列 的前
的前 项和为
项和为 ,且
,且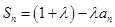 ,其中
,其中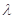 为常数,且
为常数,且
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)设数列 的公比
的公比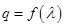 ,数列
,数列 满足
满足 ,
, (
( 求数列
求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,
,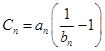 ,数列
,数列 的前
的前 项和为
项和为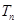
某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求出物理成绩低于50分的学生人数;
(Ⅱ)估计这次考试物理学科及格率(60分及以上为及格)
(Ⅲ)从物理成绩不及格的学生中选两人,求他们成绩至少有一个不低于50分的概率.
在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且
(1)求角B的大小;
(2)若 ,且
,且 ,求
,求 的最小值.
的最小值.