设数列 的前
的前 项和为
项和为 ,且
,且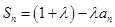 ,其中
,其中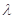 为常数,且
为常数,且
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)设数列 的公比
的公比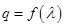 ,数列
,数列 满足
满足 ,
, (
( 求数列
求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,
,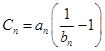 ,数列
,数列 的前
的前 项和为
项和为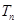
如图, 为多面体,平面
为多面体,平面 与平面
与平面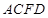 垂直,点
垂直,点 在线段
在线段 上,
上, ,
,
 ,△OAB,△OAC,△ODE,△ODF都是正三角形。
,△OAB,△OAC,△ODE,△ODF都是正三角形。
(Ⅰ)证明直线 ;
;
(Ⅱ)求棱锥 的体积.
的体积.
将一枚骰子先后抛掷两次,观察向上的点数,
(1)求点数之和是5的概率;
(2)设a,b分别是将一枚骰子先后抛掷两次向上的点数,求等式 成立的概率。
成立的概率。
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为
 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号 |
1 |
2 |
3 |
4 |
5 |
成绩 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图求这两个班的平均身高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取1同学,求身高至少为176 cm的同学被抽中的概率.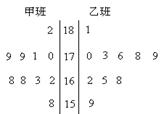
如图,从参加环保知识竞赛的学生中抽出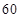 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1) 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)  这组的频率是多少?
这组的频率是多少?
(3)估计这次环保知识竞赛的及格率(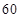 分及以上为及格)
分及以上为及格)