如图所示，半径R=0.80m的1/4光滑圆弧轨道竖直固定，过最低点的半径OC处于竖直位置．其右方有底面半径r=0.2m的转筒，转筒顶端与C等高，下部有一小孔，距顶端h=0.8m．转筒的轴线与圆弧轨道在同一竖直平面内，开始时小孔也在这一平面内的图示位置．今让一质量m=0.1kg的小物块自A点由静止开始下落后打在圆弧轨道上的B点，但未反弹，在瞬问碰撞过程中，小物块沿半径方向的分速度立刻减为O，而沿切线方向的分速度不变．此后，小物块沿圆弧轨道滑下，到达C点时触动光电装置，使转筒立刻以某一角速度匀速转动起来，且小物块最终正好进入小孔．已知A、B到圆心O的距离均为R，与水平方向的夹角均为θ=30°，不计空气阻力，g取l0m/s2．求：
（1）小物块到达C点时对轨道的压力大小 FC；
（2）转筒轴线距C点的距离L；
（3）转筒转动的角速度ω.
相隔一定距离的A，B两球质量相等，假定它们之间存在恒定的斥力作用．原来两球被按住，处在静止状态．现突然松开两球，同时给A球以速度v0，使之沿两球连线射向B球，B球初速为零．若两球间的距离从最小值(两球未接触)到刚恢复到原始值所经历的时间为t0．求B球在斥力作用下的加速度．
直升机由顶部螺旋桨向下推动空气而获得升力．如果直升机质量为M，被向下推动的空气获得的速度为v，那么直升机悬停在空中静止时螺旋桨发动机的功率是多大?
如图所示，光滑水平面上有一小车B，右端固定一沙箱，沙箱左侧连接一水平轻弹簧，小车和沙箱总质量为M．车上放有一物块A，质量也为M．物块A随小车以速度
向右匀速运动，物块A与其左侧的车面的动摩擦因数为
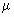，与其余部分车面间无摩擦．在车匀速运动时，距沙面H高处有一质量为m的泥球自由下落，恰好落在沙箱中，试求：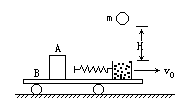
(1)小车在前进中，弹簧弹性势能的最大值是多少？
(2)为使物块A不从小车上滑下，车面粗糙部分至少应多长？
如图所示，甲、乙两小孩各乘一辆冰车在山坡前的水平冰道上游戏。甲和他的冰车总质量
=40kg，从山坡上自由下滑到水平冰道上的速度
=3m/s；乙和他的冰车总质量
=60kg，以大小为
=0.5m/s的速度迎着甲滑来，与甲相碰。若不计一切摩擦，小车也不直接接触，问相碰时，甲对乙施加的推力对乙做功在什么范围内，才能使两车分开，并且以后在原直线上运动甲、乙俩人不再相碰？（山坡与水平冰道连接处为圆弧形）
如图所示，光滑水平面上物块A质量为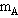
=2kg，物块B与物块C质量相同
=1kg，用一轻质弹簧将物块A与B连接，现在用力使三个物块靠近，AB间弹簧被压缩，此过程外力做功72J，然后释放，求：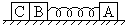
(1)当物块B与C分离时，B对C做功多少?
(2)当弹簧再次被压缩到最短而后又伸长到原长时，物块A与B的速度各多少?