设函数 ,其中向量
,其中向量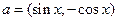 ,
, ,
,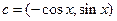 ,
, 。
。
(1)求函数 的最大值和最小正周期;
的最大值和最小正周期;
(2)将函数 的图像按向量
的图像按向量 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的 。
。
在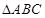 中,内角
中,内角 所对边长分别为
所对边长分别为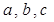 ,
,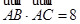 ,
,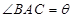 ,
,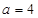 .
.
(1)求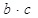 的最大值及
的最大值及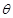 的取值范围;
的取值范围;
(2)求函数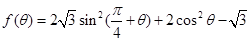 的最小值.
的最小值.
已知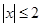 ,
,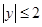 ,点
,点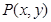 .
.
(1)求当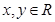 时,点
时,点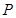 满足
满足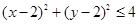 的概率;
的概率;
(2)求当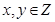 时,点
时,点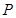 满足
满足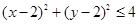 的概率
的概率
已知函数
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数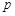 的取值范围;
的取值范围;
(Ⅲ)若 ,且至少存在一点
,且至少存在一点 ,使得
,使得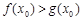 成立,求实数
成立,求实数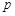 的取值范围.[
的取值范围.[
已知 ,直线
,直线 ,椭圆
,椭圆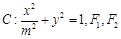 分别为椭圆
分别为椭圆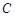 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线 过右焦点
过右焦点 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆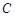 交于
交于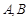 两点,
两点, 的重心分别为
的重心分别为 若原点
若原点 在以线段
在以线段 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围.
投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面出的数字分别作为点 的横坐标和纵坐标.
的横坐标和纵坐标.
(Ⅰ)求点 落在区域
落在区域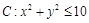 内的概率;
内的概率;
(Ⅱ)若以落在区域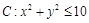 上的所有点为顶点作面积最大的多边形区域
上的所有点为顶点作面积最大的多边形区域 ,在区域
,在区域 上随机撒一粒豆子,求豆子落在区域
上随机撒一粒豆子,求豆子落在区域 上的概率.
上的概率.