(本题12分)已知关于 的不等式
的不等式 的解集为
的解集为 .
.
(1)若 ,求集合
,求集合 ;
;
(2)若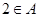 且
且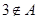 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数f(x)的定义域为R,且对m、n∈R,恒有f(m+n)=f(m)+f(n)-1,且f(-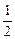 )=0,当x>-
)=0,当x>-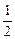 时,f(x)>0.
时,f(x)>0.
(1)求证:f(x)是单调递增函数;
(2)试举出具有这种性质的一个函数,并加以验证.
设函数f(x)的定义域关于原点对称且满足:
(i)f(x1-x2)= ;
;
(ii)存在正常数a使f(a)=1 求证:
求证:
(1)f(x)是奇函数.
(2)f(x)是周期函数,且有一个周期是4.
求证函数f(x)=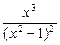 在区间(1,+∞)上是减函数.
在区间(1,+∞)上是减函数.
已知函数f(x)=ax+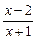 (a>1).
(a>1).
(1)证明:函数f(x)在(-1,+∞)上为增函数.
(2)用反证法证明方程f(x)=0没有负数根.
已知函数y=f(x)=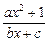 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.