已知函数y=f(x)=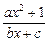 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.
已知函数 满足
满足 ,
, ,
, ;且使
;且使 成立的实数
成立的实数 只有一个。
只有一个。
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)若数列 满足
满足 ,
,
 ,
, ,
, ,证明数列
,证明数列 是等比数列,并求出
是等比数列,并求出 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明: ,
,
(本小题满分14分)如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中AC=3,AB=5,
(Ⅰ)求证:
(Ⅱ)求证:AC1//平面CDB1;
(Ⅲ)求三棱锥A1—B1CD的体积.
设计一幅宣传画,要求画面面积为 ,画面的宽与高的比为
,画面的宽与高的比为 ,画面的上
,画面的上
各留 的空白,左右各留
的空白,左右各留 的空白,问怎样确定画面的高与宽的尺寸,能使宣传画
的空白,问怎样确定画面的高与宽的尺寸,能使宣传画
所用纸张面积最小?如果 ,那么
,那么 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
已知函数
(I)若函数 的图象关于直线
的图象关于直线 对称,求a的最小值;
对称,求a的最小值;
(II)若存在 成立,求实数m的取值范围.
成立,求实数m的取值范围.
正实数数列
中,
,且
成等差数列.
(1) 证明数列
中有无穷多项为无理数;
(2)当
为何值时,
为整数,并求出使
的所有整数项的和.