设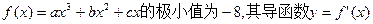
的图像经过点 如图所示, (Ⅰ)求
如图所示, (Ⅰ)求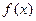 的解析式;
的解析式;
(Ⅱ)若对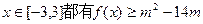 恒成立,
恒成立,
求实数m的取值范围.
(本小题满分13分)如图,在四棱锥 中,底面
中,底面 是等腰梯形,
是等腰梯形,  ∥
∥ ,
, ,
,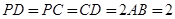 ,
,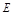 为
为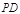 的中点.
的中点.
(Ⅰ)求证: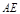 ∥平面
∥平面 ;
;
(Ⅱ)若
(ⅰ)求证平面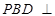 平面
平面 ;
;
(ⅱ)求直线 与底面
与底面 成角的正弦值.
成角的正弦值.
设函数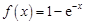 .
.
(Ⅰ)证明:当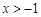 时,
时,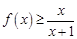 ;
;
(Ⅱ)设当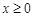 时,
时,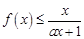 ,求实数
,求实数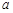 的取值范围.
的取值范围.
已知抛物线 的焦点为椭圆
的焦点为椭圆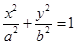
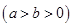 的右焦点,且椭圆的长轴长为
的右焦点,且椭圆的长轴长为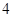 ,左右顶点分别为
,左右顶点分别为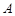 ,
,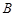 .经过椭圆左焦点的直线
.经过椭圆左焦点的直线 与椭圆交于
与椭圆交于 、
、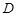 两点.
两点.
(Ⅰ)求椭圆标准方程;
(Ⅱ)记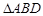 与
与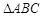 的面积分别为
的面积分别为 和
和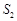 ,且
,且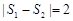 ,求直线
,求直线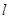 的方程;
的方程;
(Ⅲ)若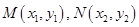 是椭圆上的两动点,且满足
是椭圆上的两动点,且满足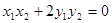 ,动点
,动点 满足
满足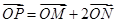 (其中
(其中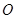 为坐标原点),求动点
为坐标原点),求动点 的轨迹方程.
的轨迹方程.
已知正项数列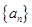 ,
,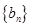 满足:对任意正整数
满足:对任意正整数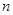 ,都有
,都有 ,
,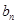 ,
, 成等差数列,
成等差数列,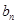 ,
, ,
,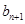 成等比数列,且
成等比数列,且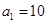 ,
,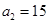 .
.
(Ⅰ)求证:数列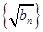 是等差数列;
是等差数列;
(Ⅱ)求数列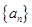 ,
,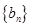 的通项公式;
的通项公式;
(Ⅲ)设 =
= +
+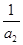 +…+
+…+ ,如果对任意的正整数
,如果对任意的正整数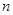 ,不等式
,不等式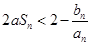 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图:已知矩形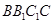 所在平面与底面
所在平面与底面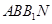 垂直,直角梯形
垂直,直角梯形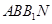 中
中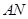 //
// ,
,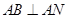 ,
,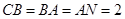 ,
,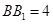 .
.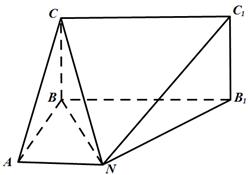
(Ⅰ)求证: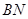
 ;
;
(Ⅱ)求二面角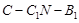 的正弦值;
的正弦值;
(Ⅲ)在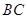 边上找一点
边上找一点 ,使
,使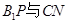 所成角的余弦值为
所成角的余弦值为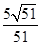 ,并求线段
,并求线段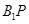 的长.
的长.