已知函数 ,其中
,其中 .
.
(1)当 时,求函数f(x)的最大值; (2)讨论函数f(x)的单调性.
时,求函数f(x)的最大值; (2)讨论函数f(x)的单调性.
如图,BA是圆O的直径,延长BA至E,使得AE=AO,过E点作圆O的割线交圆O于D、E,使AD=DC,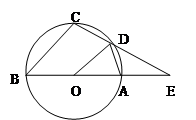
求证: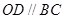 ;
;
若ED=2,求圆O的内接四边形ABCD的周长。
已知函数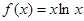 ,
,
(1)求函数 在
在 上的最小值;
上的最小值;
(2)若函数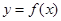 与
与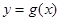 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;
(3)若函数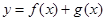 有两个不同的极值点
有两个不同的极值点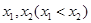 ,且
,且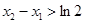 ,求实数a的取值范围。
,求实数a的取值范围。
已知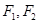 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P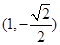 在椭圆上,线段
在椭圆上,线段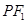 与y轴的交点M满足
与y轴的交点M满足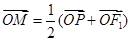
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 圆O是以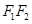 为直径的圆,直线
为直径的圆,直线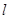 :
: 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点 ,当
,当 ,且满足
,且满足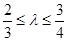 时,求直线
时,求直线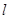 的方程。
的方程。
如图,将边长为2的正方形ABCD沿对角线BD折叠,使的平面ABD⊥平面CBD,AE⊥平面ABD,且AE= ,
,
(1) 求证:DE⊥AC
(2)求DE与平面BEC所成角的正弦值
(3)直线BE上是否存在一点M,使得CM//平面ADE,若存在,求M的位置,不存在,请说明理由。
为了防止受到核污染的产品影响我国民众的身体健康,要求产品进入市场前必须进行两轮核放射检测,只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响。
,两轮检测是否合格相互没有影响。
(1)求该产品不能销售的概率
(2)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元)。已知一箱中有4件产品,记可销售的产品数为X,求X的分布列,并求一箱产品获利的均值。