求下列椭圆的焦距。
(1)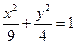 ;(2)
;(2)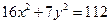 。
。
如图,在三棱柱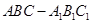 中,
中,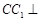 底面
底面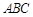 ,
,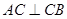 ,点
,点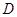 是
是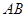 的中点.
的中点.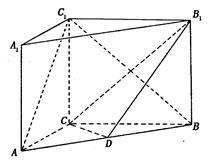
(Ⅰ)求证: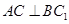 ;
;
(Ⅱ)求证: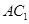 ∥平面
∥平面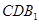 .
.
(Ⅲ)设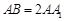 ,
,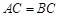 ,在线段
,在线段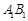 上是否存在点
上是否存在点 ,使得
,使得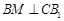 ?若存在,确定点
?若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
设等差数列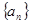 的前
的前 项和为
项和为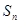 ,
,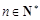 ,公差
,公差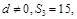 已知
已知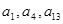 成等比数列.
成等比数列.
(Ⅰ)求数列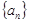 的通项公式;
的通项公式;
(Ⅱ)设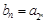 ,求数列
,求数列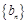 的前
的前 项和
项和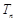 .
.
已知实数数列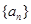 满足:
满足: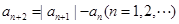 ,
,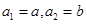 ,记集合
,记集合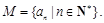
(Ⅰ)若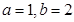 ,用列举法写出集合
,用列举法写出集合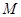 ;
;
(Ⅱ)若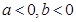 ,判断数列
,判断数列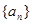 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(Ⅲ)若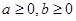 ,且
,且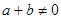 ,求集合
,求集合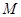 的元素个数的最小值.
的元素个数的最小值.
已知函数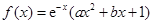 (其中
(其中 是常数,
是常数,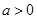 ,
,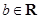 ),函数
),函数 的导函数为
的导函数为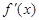 ,且
,且 .
.
(Ⅰ)若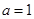 ,求曲线
,求曲线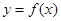 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当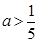 时,若函数
时,若函数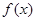 在区间
在区间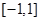 上的最大值为
上的最大值为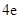 ,试求
,试求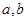 的值.
的值.
已知函数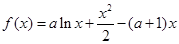 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当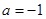 时,证明
时,证明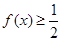 .
.