已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-ax2(a>0)的一部分,栏栅与矩形区域的边界交于点M、N,交曲线于点P,设P(t,f(t)).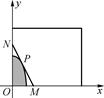
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t);
(2)若在t=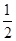 处,S(t)取得最小值,求此时a的值及S(t)的最小值.
处,S(t)取得最小值,求此时a的值及S(t)的最小值.
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(km/h)是车流密度x(辆/千米)的函数.当桥上的车流密度达到200辆/km时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/km时,车流速度为60km/h,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出其最大值.(精确到1辆/小时)
某公司为一家制冷设备厂设计生产某种型号的长方形薄板,其周长为4m.这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.
(1)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=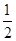 AB,tan∠FED=
AB,tan∠FED=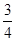 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.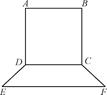
(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?