已知点A(1,0)、B(0,2)、C(-1,-2),求以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
设两个非零向量e1和e2不共线.
(1)如果 =e1-e2,
=e1-e2, =3e1+2e2,
=3e1+2e2,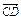 =-8e1-2e2,
=-8e1-2e2,
求证:A、C、D三点共线;
(2)如果 =e1+e2,
=e1+e2, =2e1-3e2,
=2e1-3e2,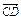 =2e1-ke2,且A、C、D三点共线,求k的值.
=2e1-ke2,且A、C、D三点共线,求k的值.
已知点G为△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且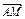 =x
=x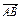 ,
, =y
=y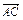 ,求
,求 +
+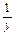 的值.
的值.
已知:任意四边形ABCD中,E、F分别是AD、BC的中点,求证: =
= (
( +
+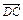 ).
).
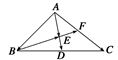
如图所示,在△ABC中,D、F分别是BC、AC的中点,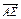 =
=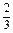
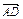 ,
,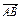 =a,
=a,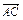 =b.
=b.
(1)用a、b表示向量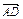 、
、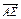 、
、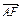 、
、 、
、 ;
;
(2)求证:B、E、F三点共线.