一个质点从静止开始做匀加速直线运动,已知它在第4s内的位移是14m,求它前72m所用的时间.
类比是研究问题的常用方法。
(1)情境1:物体从静止开始下落,除受到重力作用外,还受到一个与运动方向相反的空气阻力 (k为常量)的作用。其速率v随时间t的变化规律可用方程 (①式)描述,其中 为物体质量, 为其重力。求物体下落的最大速率 。
(2)情境2:如图1所示,电源电动势为 ,线圈自感系数为 ,电路中的总电阻为 。闭合开关 ,发现电路中电流 随时间 的变化规律与情境1中物体速率 随时间 的变化规律类似。类比①式,写出电流 随时间 变化的方程;并在图2中定性画出 图线。

(3)类比情境1和情境2中的能量转化情况,完成下表。
|
情境1 |
情境2 |
|
物体重力势能的减少量 |
|
|
物体动能的增加量 |
|
|
电阻R上消耗的电能 |
(1)如图所示,一个轻质弹簧下端挂一小球,小球静止。现将小球向下拉动距离A后由静止释放,并开始计时,小球在竖直方向做简谐运动,周期为T。经 时间,小球从最低点向上运动的距离_____ (选填“大于”、“小于”或“等于”);在 时刻,小球的动能______(选填“最大”或“最小”)。

(2)如图所示,一种光学传感器是通过接收器Q接收到光的强度变化而触发工作的。光从挡风玻璃内侧P点射向外侧M点再折射到空气中,测得入射角为 ,折射角为 ;光从P点射向外侧N点,刚好发生全反射并被Q接收,求光从玻璃射向空气时临界角 的正弦值表达式。

(1)在高空飞行的客机上某乘客喝完一瓶矿泉水后,把瓶盖拧紧。下飞机后发现矿泉水瓶变瘪了,机场地面温度与高空客舱内温度相同。由此可判断,高空客舱内的气体压强______(选填“大于”、“小于”或“等于”)机场地面大气压强:从高空客舱到机场地面,矿泉水瓶内气体的分子平均动能______(选填“变大”、“变小”或“不变”)。
(2)为方便抽取密封药瓶里的药液,护士一般先用注射器注入少量气体到药瓶里后再抽取药液,如图所示,某种药瓶的容积为0.9mL,内装有0.5mL的药液,瓶内气体压强为 ,护士把注射器内横截面积为 、长度为 、压强为 的气体注入药瓶,若瓶内外温度相同且保持不变,气体视为理想气体,求此时药瓶内气体的压强。

[物理--选修3-4]
(1)在双缝干涉实验中,用绿色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是________(最多选3个)。
| A. |
改用红色激光 |
| B. |
改用蓝色激光 |
| C. |
减小双缝间距 |
| D. |
将屏幕向远离双缝的位置移动 |
| E. |
将光源向远离双缝的位置移动 |
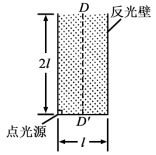
(2)一直桶状容器的高为 ,底面是边长为 l的正方形;容器内装满某种透明液体,过容器中心轴 、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的 D点射出的两束光线相互垂直,求该液体的折射率。
[物理--选修3-3]
(1)如图,用隔板将一绝热汽缸分成两部分,隔板左侧充有理想气体,隔板右侧与绝热活塞之间是真空。现将隔板抽开,气体会自发扩散至整个汽缸。待气体达到稳定后,缓慢推压活塞,将气体压回到原来的体积。假设整个系统不漏气。下列说法正确的是________(最多选3个)。

| A. |
气体自发扩散前后内能相同 |
| B. |
气体在被压缩的过程中内能增大 |
| C. |
在自发扩散过程中,气体对外界做功 |
| D. |
气体在被压缩的过程中,外界对气体做功 |
| E. |
气体在被压缩的过程中,气体分子的平均动能不变 |
(2)一热气球体积为 ,内部充有温度为 的热空气,气球外冷空气的温度为 。已知空气在1个大气压、温度 时的密度为 ,该气球内、外的气压始终都为1个大气压,重力加速度大小为 。
(i)求该热气球所受浮力的大小;
(ii)求该热气球内空气所受的重力;
(iii)设充气前热气球的质量为 ,求充气后它还能托起的最大质量。