(本题满分15分)已知数列{ }中
}中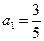 ,
,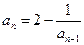 (n≥2,
(n≥2, ),数列
),数列 ,满足
,满足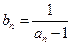 (
(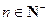 )(1)求证数列{
)(1)求证数列{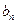 }是等差数列;(2)求数列{
}是等差数列;(2)求数列{ }中的最大项与最小项,并说明理由(3)记
}中的最大项与最小项,并说明理由(3)记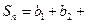 …
…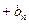 ,求
,求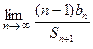 .
.
已知 是奇函数,且其图象经过点(1,3)和(2,3)。
是奇函数,且其图象经过点(1,3)和(2,3)。
(1)求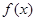 的表达式;
的表达式;
(2)用单调性的定义证明: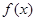 在
在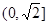 上是减函数;
上是减函数;
(3)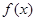 在
在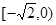 上是增函数还是减函数?(只需写出结论,不需证明)
上是增函数还是减函数?(只需写出结论,不需证明)
用抽气机每次抽出容器内空气的60%,设容器内原有空气总量为 ,用抽气机抽x次后,剩余空气总量为
,用抽气机抽x次后,剩余空气总量为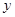
(1)写出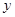 关于
关于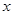 的函数关系式,并标明定义域;
的函数关系式,并标明定义域;
(2)至少抽多少次后,剩余空气总量才能不超过原有总量的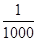 ?
?
(以下数据供你参考: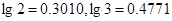 )
)
(1)求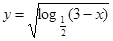 的定义域;
的定义域;
(2)已知
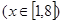 ,求函数
,求函数 的值域。
的值域。
已知 .
.
求值:(1)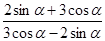 (2)
(2)
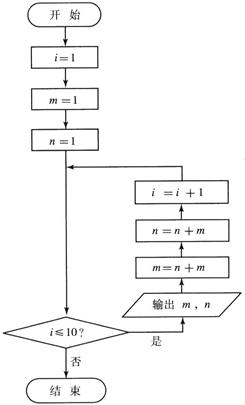
设{Fn}是斐波那契数列,其中F1=F2=1,Fn= Fn–1+Fn–2(n>2),其程序框图如右图所示是表示输出斐波那契数列的前20项的算法.请根据框图写一个程序。