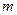 为何值时,关于
为何值时,关于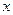 的方程
的方程 的两根:
的两根:
(1)为正数根;(2)为异号根且负根绝对值大于正根;(3)都大于1;(4)一根大于2,一根小于2;(5)两根在0,2之间。
设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
对于任意正整数n,猜想2n﹣1与(n+1)2的大小关系,并给出证明.
(Ⅰ)已知复数z=1﹣i(i是虚数单位),若z2+a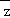 +b=3﹣3i,求实数a,b的值.
+b=3﹣3i,求实数a,b的值.
(Ⅱ)求二项式(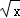 +
+ )10展开式中的常数项.
)10展开式中的常数项.
已知椭圆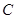 :
: 的离心率为
的离心率为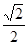 ,一条准线
,一条准线 .
.
(1)求椭圆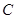 的方程;
的方程;
(2)设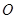 为坐标原点,
为坐标原点, 是
是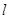 上的点,
上的点,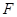 为椭圆
为椭圆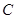 的右焦点,过点
的右焦点,过点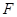 作
作 的垂线与以
的垂线与以 为直径的圆
为直径的圆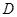 交于
交于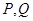 两点.
两点.
①若 =
= ,求圆
,求圆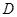 的方程;
的方程;
②若 是
是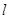 上的动点,求证:点
上的动点,求证:点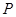 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤
(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤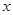 ≤200时,车流速度
≤200时,车流速度 是车流密度
是车流密度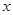 的一次函数.
的一次函数.
(Ⅰ)当0≤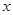 ≤200时,求函数
≤200时,求函数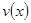 的表达式;
的表达式;
(Ⅱ)当车流密度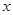 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时
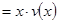 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).