某车间要在靠墙处盖一间长方形小屋，现有存砖足够砌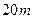
长的墙壁，问应围成怎样的长方形才能使这间小屋的面积最大？
如图，已知矩形ABCD，M，N分别是AD，BC的中点，且AM=AB，将矩形沿MN折成直二面角，若P点是线段DN上一动点，求P到BM距离的最小值。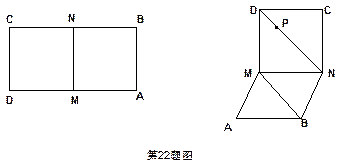
在四面体ABCD中,AB=AD=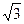
,BC=CD=3,AC=
,BD=2.
(1)平面ABD与平面BCD是否垂直？证明你的结论；（2）求二面角A-CD-B的正切值。
如图，平面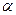
∥
，AB和AC是夹在平面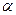与之间的两条线段，AB⊥AC，且AB=2，直线AB与平面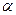所成角为30°，求线段AC长的取值范围。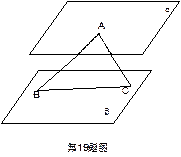
.如图，ABCD-A1B1C1D1是棱长为的正方体，M，N，P，Q，R，S分别是AA1，AB，AD，CC1，B1C1，C1D1的中点，求证：平面PMN∥平面QRS。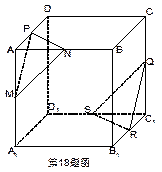
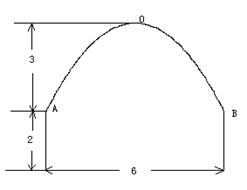
一条隧道的横断面由抛物线弧及一个矩形的三边围成，尺寸如图所示（单位：
），一辆卡车空车时能通过此隧道，现载一集装箱，箱宽3，车与箱共高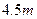
，此车是否能通过隧道？并说明理由．