一火车每小时煤消耗的费用与火车行驶的速度之立方成正比,已知当速度为每小时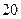 千米时,每小时消耗煤之价格为
千米时,每小时消耗煤之价格为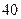 元,其他费用每小时要
元,其他费用每小时要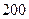 元,问火车行驶的速度如何时,才能使火车从甲城开往乙城的费用最少。(已知火车的最高速度为每小时
元,问火车行驶的速度如何时,才能使火车从甲城开往乙城的费用最少。(已知火车的最高速度为每小时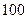 千米)
千米)
(2).选修4 - 4:坐标 系与
系与 参数方程
参数方程
以极点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位, 圆
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位, 圆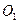 的方程为
的方程为 ,圆
,圆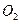 的参数方程为
的参数方程为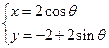 (为参数),求两圆的公共弦的长度。
(为参数),求两圆的公共弦的长度。
(本小题满分14分)
(1).选修4-2:矩阵与变换
已知矩阵 ,向量
,向量
(I)求矩阵 的特征值
的特征值 、
、 和特征向量
和特征向量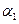 、
、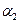 ;
;
(Ⅱ)求 的值。
的值。
本小题满分14分)
三次函数 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
(1)若函数f(x)为奇函数且过点(1,-3),当x<0时求 的最大值 ;
的最大值 ;
(2)若函数在x=1处取得极值-2,试用c表示a和b,并求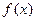 的单调递减区间;
的单调递减区间;
(3)设点A、B、C、D的横坐标分别为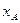 ,
,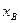 ,
, ,
,
求证 ;
;
(本小题满分13分)
已知椭圆 经过点(p,q),离心率
经过点(p,q),离心率 其中p,q分别表示标准正态分布的期望值与标准差。
其中p,q分别表示标准正态分布的期望值与标准差。
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于A,B两点,点A关于x轴的对称点为
与椭圆C交于A,B两点,点A关于x轴的对称点为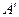
 。①试建立
。①试建立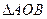 的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线
的面积关于m的函数关系;②莆田十中高三(1)班数学兴趣小组通过试验操作初步推断:“当m变化时,直线 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
如图,在三棱 柱
柱 中,已知
中,已知
 ,
,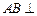 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;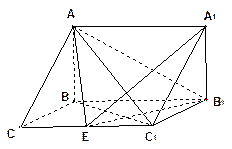
(2)在棱 (不包含端点
(不包含端点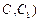 上确定一点
上确定一点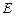 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若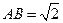 ,求二面角
,求二面角 的大小.
的大小.