如图, ,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
(Ⅲ)对于(II)中的直线l,是否存在k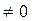 使|OF|=|OG|
使|OF|=|OG|
若有求出k的值,若没有说明理由.(O为原点)
已知向量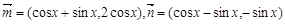 。
。
(1)求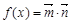 的最小正周期和单调减区间;
的最小正周期和单调减区间;
(2)将函数 的图象向右平移
的图象向右平移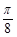 个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数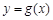 的图象,在△ABC中,角A、B、C的对边分别为
的图象,在△ABC中,角A、B、C的对边分别为 ,若
,若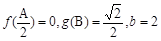 ,求
,求 的值.
的值.
已知数列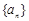 是等差数列,
是等差数列,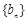 是等比数列,
是等比数列,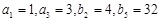 。
。
(1)求数列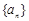 、
、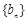 的通项公式;
的通项公式;
(2)设数列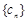 中,
中,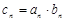 ,求数列
,求数列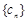 的前n项和Sn.
的前n项和Sn.
如图,菱形ABCD的边长为2,∠BAD=60º, M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).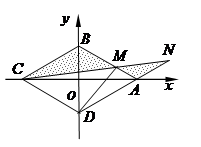
(1)试用t表示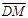 与
与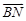 ,并求它们所成角的大小;
,并求它们所成角的大小;
(2)设f(t)=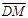 ·
·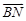 ,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数
,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数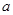 的取值范围:
的取值范围:
①存在t1,t2∈(0,1),使得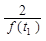 =g(t2);
=g(t2);
②对任意t1∈(0,1),恒存在t2∈(0,1),使得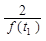 =g(t2).
=g(t2).
已知函数f(x)=x2·ln|x|(x≠0).
(1)求f(x)的最值;
(2)若关于x的方程f(x)=kx-1无实数解,求实数k的取值范围.
若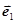 ,
,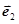 ,
,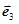 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足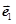 +
+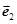 +
+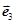 =
= ,且向量
,且向量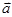 =x
=x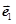 +
+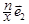 +(x+
+(x+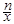 )
)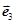 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求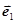 与
与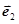 所成角的大小;
所成角的大小;
(2)记f(x)=|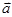 |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.