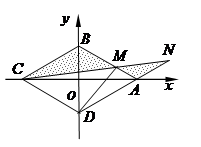
如图,菱形ABCD的边长为2,∠BAD=60º, M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
(1)试用t表示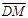 与
与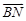 ,并求它们所成角的大小;
,并求它们所成角的大小;
(2)设f(t)=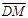 ·
·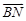 ,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数
,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数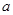 的取值范围:
的取值范围:
①存在t1,t2∈(0,1),使得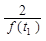 =g(t2);
=g(t2);
②对任意t1∈(0,1),恒存在t2∈(0,1),使得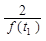 =g(t2).
=g(t2).
在直角坐标系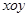 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点
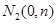 ,且
,且 .
.
(Ⅰ)求直线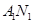 与
与 交点的轨迹
交点的轨迹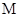 的方程;
的方程;
(Ⅱ)已知点 (
( )是轨迹
)是轨迹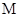 上的定点,
上的定点,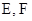 是轨迹
是轨迹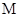 上的两个动点,如果直线
上的两个动点,如果直线 的斜率
的斜率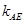 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线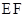 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
如图,已知△AOB,∠AOB= ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为 .
.
(Ⅰ)当平面COD⊥平面AOB时,求 的值;
的值;
(Ⅱ)当 ∈[
∈[ ,
, ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.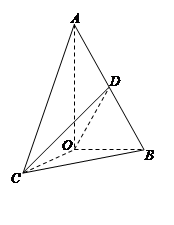
已知数列 满足:
满足:
(Ⅰ)求证:数列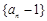 是等比数列;
是等比数列;
(Ⅱ)令 (
(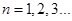 ),如果对任意
),如果对任意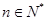 ,都有
,都有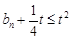 ,
,
求实数 的取值范围.
的取值范围.
已知点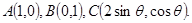
(Ⅰ)若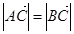 ,求
,求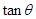 的值;
的值;
(Ⅱ)若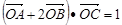 ,其中
,其中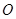 为坐标原点,求
为坐标原点,求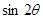 的值
的值
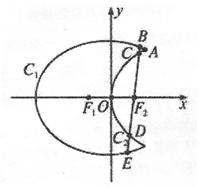
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,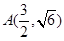 是曲线C1和C2的交点.
是曲线C1和C2的交点.
(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程;
(Ⅱ)过F2作一条与x轴不垂直的直线,分别与曲线C1、C2依次交于B、C、D、E四点,若G为CD中点,H为BE中点,问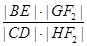 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.