.已知函数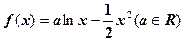 。(1)讨论函数
。(1)讨论函数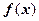 的单调性;(2)当
的单调性;(2)当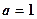 时,设
时,设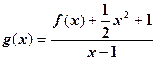 ,若
,若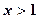 时,
时,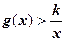 恒成立。求整数
恒成立。求整数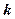 的最大值。
的最大值。
设数列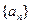 的前
的前 项和为
项和为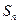 ,且方程
,且方程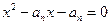 有一根为
有一根为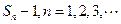 。
。
(Ⅰ)求 ;(Ⅱ)猜想数列
;(Ⅱ)猜想数列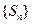 的通项公式,并给出严格的证明。
的通项公式,并给出严格的证明。
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3道题,每人答对其中2题就停止答题,即为闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是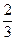 。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设乙答对题目的个数为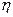 ,求
,求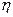 的方差;
的方差;
(Ⅲ)设甲答对题目的个数为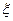 ,求
,求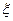 的分布列及数学期望。
的分布列及数学期望。
已知函数 在
在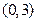 内有极值,求实数
内有极值,求实数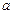 的范围。
的范围。
.设函数 且
且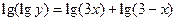 。
。
(Ⅰ)求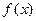 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求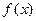 的值域。
的值域。