如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.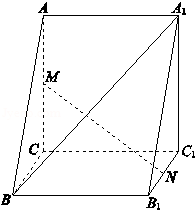
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
(本小题满分12分)
某地建一座桥,两端的桥墩已建好,这两墩相距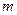 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为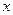 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为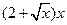 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。
万元。
(Ⅰ)试写出 关于
关于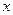 的函数关系式;
的函数关系式;
(Ⅱ)当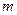 =640米时,
=640米时, 需新建多少个桥墩才能使
需新建多少个桥墩才能使 最小?
最小?
(本小题满分12分)
如图, 平面ABC,EB//DC,AC=BC=EB=2DC=2,
平面ABC,EB//DC,AC=BC=EB=2DC=2, ,P、Q分别为DE、AB的中点。
,P、Q分别为DE、AB的中点。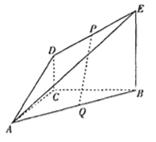
(Ⅰ)求证:PQ//平面ACD;
(Ⅱ)求几何体B—ADE的体积;
(Ⅲ)求平面ADE与平面ABC所成锐二面角的正切值。
(本小题满分12分)
已知等差数列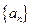 满足:
满足: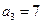 ,
, .
.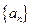 的前n项和为
的前n项和为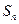
(Ⅰ)求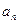 及
及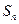 ;
;
(Ⅱ)令bn=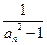 (n
(n N*),求数列
N*),求数列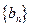 的前n项和
的前n项和 .
.
(本小题满分10分)
在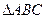 中,角
中,角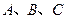 所对的边分别为
所对的边分别为 ,向量
,向量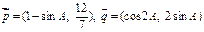 ,且
,且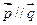 .
.
(Ⅰ)求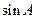 的值;
的值;
(Ⅱ)若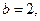
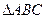 的面积为
的面积为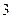 ,求
,求 .
.

