设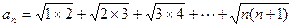 求证:
求证: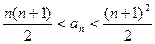
已知二次函数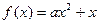 (
(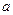
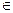 R,
R,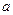
 0).(1)当0<
0).(1)当0<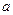 <
< 时,
时,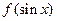 (
(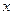
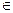 R)的最大值为
R)的最大值为 ,求
,求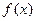 的最小值.(2)如果
的最小值.(2)如果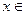 [0,1]时,总有|
[0,1]时,总有|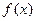 |
| .试求
.试求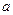 的取值范围.(3)令
的取值范围.(3)令 ,当
,当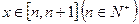 时,
时, 的所有整数值的个数为
的所有整数值的个数为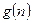 ,求证数列
,求证数列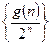 的前
的前 项的和
项的和 .
.
设经过原点O的两直线 的倾斜角分别是
的倾斜角分别是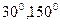 ,点A在
,点A在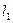 上,点B在
上,点B在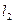 上,且
上,且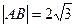 ,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点
,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点 ,且
,且 ,求点P
,求点P
锐角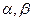 满足:
满足: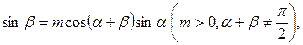 令
令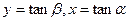
(1)把 表示成
表示成 的不含
的不含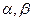 的函数
的函数 (即写出
(即写出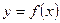 的解析式)(2)当
的解析式)(2)当 时,求函数
时,求函数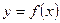 的最大值。
的最大值。
在数列 中,
中, ,
, (1)证明数列
(1)证明数列 是等比数列;(2)求数列
是等比数列;(2)求数列 的前
的前 项和
项和 ;(3)若不等式
;(3)若不等式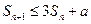 对任意
对任意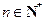 都成立,求
都成立,求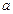 的最小值。
的最小值。
△ABC顶点A(1, 1), B(-2, 10), C(3, 7)ÐBAC平分线交BC边于D,求D点坐标