四棱锥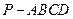 中,底面ABCD是一个平行四边形,
中,底面ABCD是一个平行四边形, ,
, ,
,
(1)求四棱锥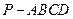 的体积;
的体积;
(2)定义 =
=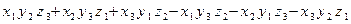 ,对于向量
,对于向量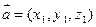 ,
,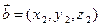 ,
, 有
有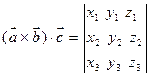 ,
,
则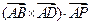 =__________.
=__________.
在△ABC中,已知内角A.B.C所对的边分别为a.b.c,且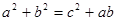
(1) 若 ,且
,且 ,求
,求 的面积;
的面积;
(2)已知向量 (sinA,cosA),
(sinA,cosA), (cosB,-sinB),求|
(cosB,-sinB),求| |的取值范围
|的取值范围
在平面直角坐标系中,已知焦距为4的椭圆 的左、右顶点分别为
的左、右顶点分别为 ,椭圆
,椭圆 的右焦点为
的右焦点为 ,过
,过 作一条垂直于
作一条垂直于 轴的直线与椭圆相交于
轴的直线与椭圆相交于 ,若线段
,若线段 的长为
的长为 。
。
(1)求椭圆 的方程;
的方程;
(2)设 是直线
是直线 上的点,直线
上的点,直线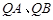 与椭圆
与椭圆 分别交于点
分别交于点 ,求证:直线
,求证:直线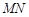 必过
必过 轴上的一定点,并求出此定点的坐标;
轴上的一定点,并求出此定点的坐标;
已知定义在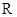 上的函数
上的函数 ,其中
,其中 为大于零的常数.
为大于零的常数.
(Ⅰ)当 时,令
时,令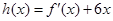 ,
,
求证:当 时,
时, (
( 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数 ,在
,在 处取得最大值,求
处取得最大值,求 的取值范围
的取值范围
已知函数 (x≠0)各项均为正数的数列{an}中a1=1,
(x≠0)各项均为正数的数列{an}中a1=1,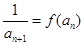 ,
,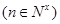 。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·
。(1)求数列{an}的通项公式;(2)在数列{bn}中,对任意的正整数n,bn·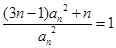 都成立,设Sn为数列{bn}的前n项和试比较Sn与
都成立,设Sn为数列{bn}的前n项和试比较Sn与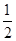 的大小。
的大小。
下面一组图形为三棱锥P-ABC的底面与三个侧面.已知AB⊥BC,PA⊥AB,PA⊥AC.
(1)在三棱锥P-ABC中,求证:平面ABC⊥平面PAB;
(2)在三棱锥P-ABC中,M是PA的中点,且PA=BC=3,AB=4,求三棱锥P-MBC的体积.