(满分14分)一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
(1)如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
(2)如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?
|
已知 的三个顶点的坐标为
的三个顶点的坐标为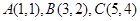 .
.
(1)求边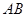 上的高所在直线的方程;
上的高所在直线的方程;
(2)若直线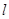 与
与 平行,且在
平行,且在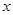 轴上的截距比在
轴上的截距比在 轴上的截距大1,求直线
轴上的截距大1,求直线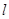 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
设数列 的首项
的首项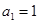 ,前
,前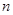 项和为
项和为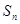 ,且
,且 ,
,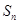 ,
,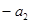 成等差数列,其中
成等差数列,其中 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 满足:
满足: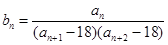 ,记数列
,记数列 的前
的前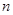 项和为
项和为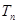 ,求
,求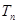 及数列
及数列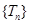 的最大项.
的最大项.
如图,已知四棱锥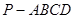 的底面为菱形,
的底面为菱形,
 面
面 ,且
,且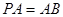 ,
, ,
,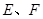 分别是
分别是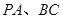 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)过 作一平面交棱
作一平面交棱 于点
于点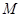 ,若二面角
,若二面角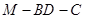 的大小为
的大小为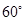 ,求
,求 的值.
的值.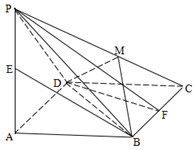
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数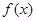 与时刻
与时刻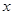 (时)的关系为
(时)的关系为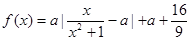 ,
,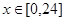 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且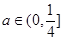 ,用每天
,用每天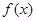 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作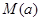 .
.
(1)令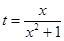 ,
,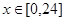 ,求
,求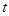 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
在 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
.
(1)求角 ;
;
(2)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.