在长方体AC¢中，已知底面两邻边AB和BC的长分别为3和4，对角线BD¢与平面ABCD所成的角为45
0，求：
（1）长方体AC¢的高；
（2）长方体AC¢的表面积；
（3）几何体C¢D¢-ABCD的体积.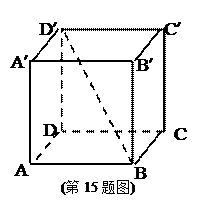
已知椭圆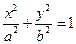
的焦点坐标为
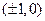，椭圆经过点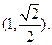
（1）求椭圆方程；
（2）过椭圆左顶点M（-a，0）与直线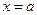
上点N的直线交椭圆于点P，求
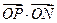的值。
（3）过右焦点且不与对称轴平行的直线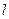
交椭圆于A、B两点，点
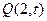，若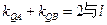
的斜率无关，求t的值
已知函数
是函数
的导函数，其中实数a是不等1的常数。
（1）设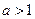
，讨论函数在区间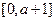
内零点的个数；
（2）求证：当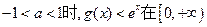
内恒成立。
如图，四棱锥P—ABCD的底面ABCD是边长为2的菱形，
，点M
是棱PC的中点，
平面ABCD，AC、BD交于点O。
（1）求证：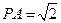
，求证：AM
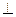平面PBD；
（2）若二面角M—AB—D的余弦值等于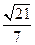
，求PA的长
袋子中有相同大小的红球3个及白球4个，现从中随机取球。
（1）取球3次，每次取后放回，求取到红球至少2次的概率；
（2）现从袋子中逐个不放回的取球，若取到红球则继续取球，取到白球则停止取球，求取球次数
的分布列与均值。
满足
，且有
