一个质量为M的雪橇静止在水平雪地上，一条质量为m的爱斯基摩狗站在该雪橇上.狗向雪橇的正后方跳下，随后又追赶并向前跳上雪橇；其后狗又反复地跳下、追赶并跳上雪橇.狗与雪橇始终沿一条直线运动.若狗跳离雪橇时雪橇的速度为v，则此时狗相对于地面的速度为v+u（其中u为狗相对于雪橇的速度，v+u为代数和，若以雪橇运动的方向为正方向，则v为正值，u为负值）.设狗总以速度v追赶和跳上雪橇，雪橇与雪地间的摩擦忽略不计.已知v的大小为5 m/s，u的大小为4 m/s，M="30" kg，m="10" kg.求：
（1）狗第一次跳上雪橇后两者的共同速度的大小；
（2）雪橇的最终速度和狗最多能跳上雪橇的次数.
（供使用但不一定用到的对数值：lg2=0.301，lg3=0.477）
如图所示，在半径为R，质量分布均匀的某星球表面，有一倾斜角为
的斜坡．以初速度
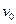向斜坡水平抛出一个小球．测得经过时间t，小球垂直落在斜坡上的C点。求：
（1）小球落到斜坡上时的速度大小v；
（2）该星球表面附近的重力加速度g；
（3）卫星绕该星球表面做匀速圆周运动的速度
。
如图所示，AB为水平轨道，A、B间距离x="2.25" m ，BCD是半径为R＝0.40 m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点。一小物块质量为m="1." 2 kg，它与水平轨道和半圆形轨道间的动摩擦因数均为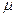
=" 0." 20。小物块在F="12" N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，小物块刚好能到达D点，g取10 
，试求：
（1）撤去F时小物块的速度大小；
（2）在半圆形轨道上小物块克服摩擦力做的功。
如图所示，把一个质量m="1" kg的物体通过两根等长的细绳与竖直杆上A、B两个固定点相连接，绳a、b长都是1 m。AB长度是1.6 m，直杆和球旋转的角速度等于多少时，b绳上才有张力？
如图所示，水平台面AB距地面的高度h＝0.8m。有一滑块从A点以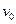
＝6m/s的初速度在台面上做匀变速直线运动，滑块与平台间的动摩擦因数
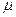=0.25。滑块运动到平台边缘的B点后水平飞出。己知AB＝2.2m。不计空气阻力，g取10
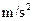。求
（1）滑块从B点飞出时的速度大小；
（2）滑块落地点到平台边缘的水平距离。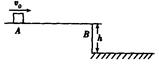
在同一平台上的O点抛出的3个物体，做平抛运动的轨迹均在纸面内，如图所示，则3个物体做平抛运动的初速度
的关系及落地时间
的关系分别是（）
A． |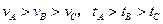
B． |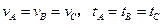
C． |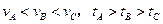
D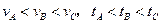． |