为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积 的金属板,间距
的金属板,间距 ,当连接到
,当连接到 的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒
的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒 个,假设这些颗粒都处于静止状态,每个颗粒带电量为
个,假设这些颗粒都处于静止状态,每个颗粒带电量为 ,质量为
,质量为 ,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
(1)经过多长时间烟尘颗粒可以被全部吸附?
(2)除尘过程中电场对烟尘颗粒共做了多少功?
(3)经过多长时间容器中烟尘颗粒的总动能达到最大?
如图1所示,电灯悬挂于两干墙之间,使连接点A上移,但保持O点位置不变,则在A点向上移动的过程中,绳OA、OB的拉力如何变化?
用劲度系数k=500N/m的轻弹簧,水平拉一木板使它沿水平桌面做匀速直线运动,弹簧长度L1=12cm.若在木板上加一个质量m=5kg的铁块,仍用原弹簧拉住它沿水平桌面做匀速直线运动,弹簧的长度L2=14cm,则木板与水平桌面间的动摩擦因数为多少?(g取10m/s2)
某一长直的赛道上,有一辆F1赛车前方200m处有一安全车正以10m/s的速度匀速前进,这时赛车从静止出发以2m/s2的加速度追赶。试求:
(1)赛车出发3s末的瞬时速度大小。
(2)赛车何时追上安全车?
(3)赛车追上安全车之前何时与安全车距离最远?
利用如图7所示的装置测量滑块和滑板间的动摩擦因数。将质量为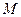 的滑块
的滑块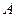 放在倾斜滑板
放在倾斜滑板 上,
上,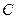 为位移传感器,它能将滑块
为位移传感器,它能将滑块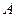 到传感器
到传感器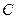 的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块
的距离数据实时传送到计算机上,经计算机处理后在屏幕上显示出滑块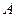 的速度——时间(
的速度——时间(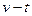 )图像。先给滑块
)图像。先给滑块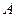 一个沿滑板
一个沿滑板 向上的初速度,得到的
向上的初速度,得到的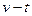 如图8所示,求:
如图8所示,求:
(1)滑块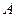 上滑时加速度的大小;
上滑时加速度的大小;
(2)滑块与滑板之间的动摩擦因数(取重力加速度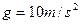 )。
)。
)如图11所示,倾角30°的光滑斜面上,并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,一个劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值。