已知圆C过定点A(0,p)(p>0),圆心C在抛物线x2=2py上运动,若MN为圆C在x轴上截得的弦,设|AM|=m,|AN|=n,∠MAN=θ.
(1)当点C运动时,|MN|是否变化?写出并证明你的结论?
(2)求 +
+ 的最大值,并求取得最大值时θ的值和此时圆C的方程.若不存在,说明理由
的最大值,并求取得最大值时θ的值和此时圆C的方程.若不存在,说明理由
已知函数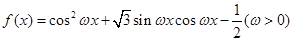 的最小正周期为
的最小正周期为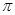 .
.
(I)求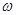 值及
值及 的单调递增区间;
的单调递增区间;
(II)在△ 中,
中,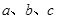 分别是三个内角
分别是三个内角 所对边,若
所对边,若 ,
, ,
,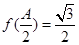 ,求
,求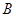 的大小.
的大小.
如图:已知方程为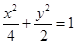 的椭圆,
的椭圆,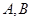 为顶点,过右焦点的弦
为顶点,过右焦点的弦 的长度为
的长度为 ,中心
,中心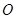 到弦
到弦 的距离为
的距离为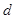 ,点
,点 从右顶点
从右顶点 开始按逆时针方向在椭圆上移动到
开始按逆时针方向在椭圆上移动到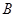 停止,当
停止,当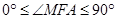 时,记
时,记 ,当
,当 ,记
,记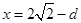 ,函数
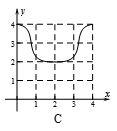
,函数 图像是 ( )
图像是 ( )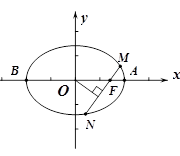



(本小题满分10分)选修4-5:不等式选讲
设函数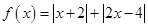 ,
, .
.
(1)当 时,解不等式
时,解不等式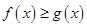 ;
;
(2)画出函数 的图象,根据图象求使
的图象,根据图象求使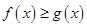 恒成立的实数
恒成立的实数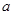 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
(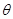 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 的左、右焦点.
的左、右焦点.
(1)以坐标原点为极点, 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线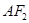 的直线
的直线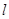 的极坐标方程;
的极坐标方程;
(2)设(1)中直线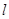 与圆锥曲线
与圆锥曲线 交于
交于 两点,求
两点,求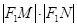 .
.
(本小题满分10分)选修4-1:几何证明选讲
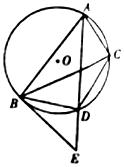
如图,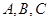 为
为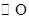 上的三个点,
上的三个点, 是
是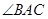 的平分线,交
的平分线,交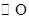 于点
于点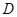 ,过
,过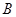 作
作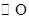 的切线交
的切线交 的延长线于点
的延长线于点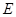 .
.
(1)证明: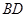 平分
平分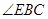 ;
;
(2)证明: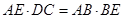 .
.