判断下列问题是排列问题还是组合问题?并计算出结果.
有 八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
八个质数:①从中任取两个数求它们的商可以有多少种不同的商?②从中任取两个求它的积,可以得到多少个不同的积?
将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时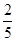 小时,种植一捆沙棘用时
小时,种植一捆沙棘用时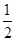 小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨仍用时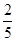 小时,而每名志愿者种植一捆沙棘实际用时
小时,而每名志愿者种植一捆沙棘实际用时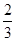 小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
已知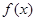 在定义域上是奇函数,且在
在定义域上是奇函数,且在 上是减函数,图像如图所示.
上是减函数,图像如图所示.
(1)化简: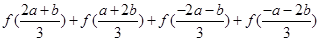 ;
;
(2)画出函数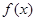 在
在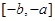 上的图像;
上的图像;
(3)证明: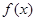 在
在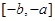 上是减函数.
上是减函数.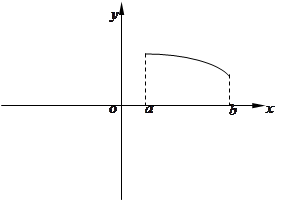
已知全集 ,集合
,集合 ,
,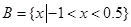 ,求:
,求:
(1)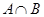 及
及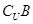 ;
;
(2)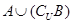 .
.
(本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x |
2 |
4 |
5 |
6 |
8 |
| 销售额y |
30 |
40 |
60 |
50 |
70 |
(1)画出数据对应的散点图,你能从散点图中发现某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律吗?
(2)求y关于x的回归直线方程;
(3)预测当广告费支出为2(百万元)时,则这种产品的销售额为多少(百万元)
某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律:
(本小题满分12分)一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率