风力发电作为一种无污染、低成本的电力产业,发展前景广阔.我国风力资源丰富,到2000年底,我国风力发电机的总装机容量已达264万千瓦.风力发电的原理是利用风推动叶轮转动,将风的动能转化为叶轮的动能,再将叶轮的动能转化为电能.
(1)设空气的密度为ρ,叶轮每个车叶的长度均为L,正对叶轮的水平风速为v,整个发电机的效率为η,那么每台发电机发出的电功率P=_____________.
(2)我国研制Wd646型风力发电机,每个车叶的长度L="22" m,当风速达到v="15" m/s时,其输出的电功率可达P="600" kW.求该风力发电机将风的动能转化为电能的总效率η.(空气密度ρ="1.29" kg/m3)
“嫦娥一号”卫星开始绕地球做椭圆轨道运动,经过变轨、制动后,成为一颗绕月球做圆轨道运动的卫星。设卫星距月球表面的高度为h,做匀速圆周运动的周期为T。已知月球半径为R,引力常量为G。(球的体积公式V=πR3,其中R为球的半径)求:
(1)月球的质量M;
(2)月球表面的重力加速度g;
(3)月球的密度ρ。
一水平传送带以v1=2m/s的速度匀速运动,将一粉笔头无初速度放在传送带上,达到相对静止时产生的划痕长L1=4m。现在让传送带以a2=1.5m/s2的加速度减速,将该粉笔头无初速度放在传送带上,求粉笔头在传送带上的划痕长度L2。求粉笔头相对传送带运动的位移L2。(取g=10m/s2)
物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB.用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示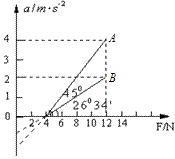
(1)利用图象求出两个物体的质量mA和mB.
甲同学分析的过程是:从图象中得到F=12N时,A物体的加速度aA=4m/s2,B物体的加速度aB=2m/s2,根据牛顿定律导出: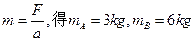 ;
;
乙同学的分析过程是:从图象中得出直线A、B的斜率为:kA=tan45°=1,kB=tan26°34′=0.5,而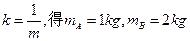 .
.
请判断甲、乙两个同学结论的对和错,并分析错误的原因.如果两个同学都错,分析各自的错误原因后再计算正确的结果.
(2)根据图象计算A、B两物体与水平面之间动摩擦因数μA和μB的数值.
今年春节前后,我国南方大部分省区遭遇了罕见的雪灾,此次灾害过程造成17个省(区、市、兵团)不同程度受灾。尤其是雪灾天气造成输电线被厚厚的冰层包裹(如图甲),使相邻两个铁塔间的拉力大大增加,导致铁塔被拉倒、压塌(如图乙),电力设施被严重损毁,给这些地方群众的生产生活造成了极大不便和巨大损失。当若干相同铁塔等高、等距时,可将之视为如图所示的结构模型。已知铁塔(左右对称)质量为m,塔基宽度为d。相邻铁塔间输电线的长度为L,其单位长度的质量为m0,输电线顶端的切线与竖直方向成θ角。已知冰的密度为ρ,设冰层均匀包裹输电线上,且冰层的横截面为圆形,其半径为R(输电线的半径可忽略)。
(1)每个铁塔塔尖所受的压力将比原来增大多少?
(2)被冰层包裹后,输电线在最高点、最低点所受的拉力大小分别为多少?
如图,原长分别为L1和L2,劲度系数分别为k1和k2的轻质弹簧竖直地悬挂在天花板上,两弹簧之间有一质量为m1的物体,最下端挂着质量为m2的另一物体,整个装置处于静止状态。现用一个质量为m的平板把下面的物体竖直地缓慢地向上托起,直到两个弹簧的总长度等于两弹簧原长之和,这时托起平板竖直向上的力是多少?m2上升的高度是多少?