如图所示,一玩滚轴溜冰的小孩(可视作质点)质量为m=30kg,他在左侧平台上滑行一段距离后平抛,恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,并沿轨道下滑,A、B为圆弧两端点,其连线水平.已知圆弧半径为R=1.0m,对应圆心角为θ=1060,平台与AB连线的高度差为h=0.8m.(计算中取g=10m/s2,sin530=0.8,cos530=0.6)求:
(1)小孩平抛的初速度
(2)小孩运动到圆弧轨道最低点O时对轨道的压力
 一小球作平抛运动,在下落过程中刚好能通过宽为L,高为H的长方形窗户ABCD的对角A和C,所用时间为T,重力加速度为g。求①小球从抛出到经过窗户的上边缘所用的时间。②小球通过C点的速度大小。
一小球作平抛运动,在下落过程中刚好能通过宽为L,高为H的长方形窗户ABCD的对角A和C,所用时间为T,重力加速度为g。求①小球从抛出到经过窗户的上边缘所用的时间。②小球通过C点的速度大小。
如图14所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动.求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2).某同学对此题的解法为:小球沿斜面运动,则 由此可求得落地的时间t.问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果.
由此可求得落地的时间t.问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果.
A、B两小球同时从距地面高为h=15m处的同一点抛出,初速度大小均为10m/s。A球竖直向下抛出,B球水平抛出,空气阻力不计,重力加速度g=10m/s2。求:
(1)A球经多长时间落地?
(2)A球落地时,A、B两球相距多远?
抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)
(1)若球在球台边缘O点正上方高度为h1处以速度 水平发出,落在球台的P1点(如图实线所示),求P1点距O点的距离x1.
水平发出,落在球台的P1点(如图实线所示),求P1点距O点的距离x1.
(2)若球在O点正上方以速度 水平发出,恰好在最高点时越过球网落在球台的P2(如图虚线所示),求
水平发出,恰好在最高点时越过球网落在球台的P2(如图虚线所示),求 的大小.
的大小.
(3)若球在O正上方水平发出后,球经反弹恰好越过球网且刚好落在对方球台边缘P3,求发球点距O点的高度h3.
如图所示,在倾角为θ的斜面顶端A处以速度v0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求: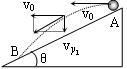
(1)小球从A运动到B处所需的时间、落到B点的速度及A、B间的距离.
(2)从抛出开始计时,经过多长时间小球离斜面的距离达到最大?这个最大距离是多少?