已知函数f(x)=ax2+ax和g(x)=x-a,其中aÎR且a¹0．
（1）若函数f(x)与g(x)的图像的一个公共点恰好在x轴上,求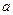
的值；
（2）若函数f(x)与g(x)图像相交于不同的两点A、B,O为坐标原点,试问：△OAB的面积S有没有最值?如果有,求出最值及所对应的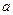的值；如果没有,请说明理由．
（3）若p和q是方程f(x)=g(x)的两根,且满足0<p<q<,证明：当xÎ(0,p)时,g(x)<f(x)<p-a.．
（本小题满分12分）
设函数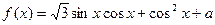
．
（1）写出函数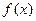
的最小正周期及单调递减区间；
（2）当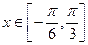
时，函数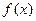的最大值与最小值的和为
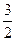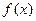，求的图象、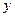
轴的正半轴及x轴的正半轴三者围成图形的面积．
若直线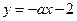
与连接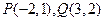
两点的线段有交点，求实数
的取值范围．
已知在□ABCD中，点A（1，1），B（2，3），CD的中点为E（4，1），将
□ABCD按向量a平移，使C点移到原点O.
（1）求向量a；
（2）求平移后的平行四边形的四个顶点的坐标.
（本小题满分12分）
已知函数
.
（Ⅰ）当
时，
使不等式
，求实数
的取值范围；
（Ⅱ）若在区间
上，函数
的图象恒在直线
的下方，求实数
的取值范围.
（本小题满分14分）
已知数列
的前
项和为
，对一切正整数，点
都在函数
的图象上，且在点处的切线的斜率为
.
（Ⅰ）求数列的通项公式；
（Ⅱ）若
，求数列
的前项和
；
（Ⅲ）设
，
，等差数列
的任一项
，其中
是
中最小的数，
，求数列的通项公式.