设函数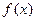 的定义域为
的定义域为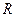 ,若存在常数
,若存在常数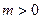 ,使
,使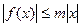 对一切实数
对一切实数 均成立,则称
均成立,则称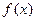 为
为 函数.给出下列函数:
函数.给出下列函数:
①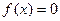 ;②
;②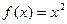 ;③
;③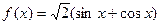 ;④
;④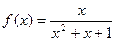 ;⑤
;⑤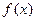 是定义在
是定义在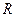 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数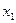 、
、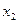 均有
均有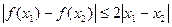 .其中是
.其中是 函数的序号为 。
函数的序号为 。
(1)证明不等式: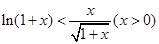
(2)已知函数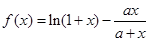 在
在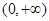 上单调递增,求实数
上单调递增,求实数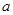 的取值范围。
的取值范围。
(3)若关于x的不等式 在
在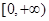 上恒成立,求实数
上恒成立,求实数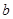 的最大值。
的最大值。
设平面内两定点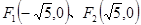 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值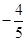 ;
;
(Ⅰ)求动点P的轨迹C1的方程;
(Ⅱ)设M(0,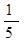 ),N为抛物线C2:
),N为抛物线C2: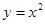 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求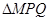 面积的最大值.
面积的最大值.
各项为正数的数列 的前n项和为
的前n项和为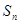 ,且满足:
,且满足: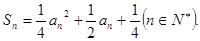
(1)求 ;
;
(2)设函数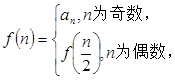
 求数列
求数列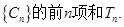
已知直三棱柱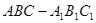 的三视图如图所示,且
的三视图如图所示,且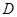 是
是 的中点.
的中点.
(Ⅰ)求证: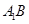 ∥平面
∥平面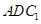 ;
;
(Ⅱ)求二面角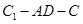 的余弦值;
的余弦值;
(Ⅲ)试问线段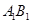 上是否存在点
上是否存在点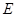 ,使
,使 与
与 成
成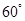 角?若存在,确定
角?若存在,确定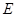 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
中国 黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有湖北师范学院的“高个子”才能担任“兼职导游”。
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用 表示所选志愿者中能担任“兼职导游”的人数,试写出
表示所选志愿者中能担任“兼职导游”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。