(本小题满分12分)在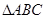 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
, .
.
(1)求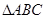 的面积;
的面积;
(2)若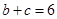 ,求
,求 的值.
的值.
(本小题满分10分)已知定点 ,直线
,直线 (
(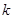 为常数).
为常数).
(1)若求实数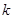 的值;
的值;
(2)以 为直径的圆与直线
为直径的圆与直线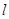 相交所得的弦长为
相交所得的弦长为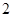 ,求实数
,求实数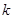 的值.
的值.
(本小题满分10分)
已知函数 的定义域为
的定义域为 .
.
(1)求实数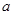 的取值范围;
的取值范围;
(2)当正数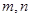 满足
满足 时,求
时,求 的最小值.
的最小值.
(本小题满分10分)
已知在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 为参数).
为参数).
(1)以原点为极点、 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆 的极坐标方程;
的极坐标方程;
(2)直线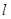 的坐标方程是
的坐标方程是 ,且直线
,且直线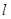 与圆
与圆 交于
交于 两点,试求弦
两点,试求弦 的长.
的长.
(本小题满分10分)
自圆 外一点
外一点 引圆
引圆 的两条割线
的两条割线 和
和 ,如图所示,其中割线
,如图所示,其中割线 过圆心
过圆心 ,
, .
.
(1)求 的大小;
的大小;
(2)分别求线段 和
和 的长度.
的长度.