(本小题满分14分)
如图,三棱锥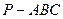 中,
中, ,
, .
.
(Ⅰ)求证: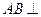 平面
平面 ;
; (Ⅱ)若
(Ⅱ)若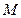 为线段
为线段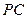 上的点,设
上的点,设 ,问
,问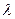 为何值时能使
为何值时能使
直线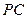
 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(本小题满分12分)
已知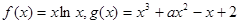 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)对一切的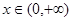 时,
时,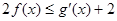 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知命题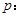 方程
方程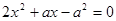 在
在 上有解,命题
上有解,命题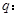 只有一个实数
只有一个实数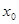 满足不等式
满足不等式 ,若命题“
,若命题“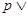
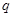 ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数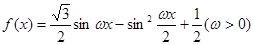 的最小正周期为
的最小正周期为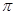 .
.
(Ⅰ)求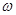 的值及函数
的值及函数 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,求函数
时,求函数 的取值范围.
的取值范围.
(本小题满分12分)已知函数
 ,
, .
.
(1)判断 在区间
在区间 上单调性;
上单调性;
(2)若 ,函数
,函数 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的解析式,并判断
的解析式,并判断 是否有最大值和最小值,请说明理由(参考数据:
是否有最大值和最小值,请说明理由(参考数据: ).
).
(本小题满分12分)已知函数 .
.
(1)若函数 在
在 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(2)已知函数 ,对于任意
,对于任意 ,总存在
,总存在 ,使得
,使得 成立,求正实数
成立,求正实数 的取值范围.
的取值范围.